Trie and Radix Tree

In the context of databases, Tries and Radix Trees are efficient data structures used for tasks like string matching, prefix searching, and indexing. These data structures provide fast operations, such as searching, insertion, and deletion, particularly in applications involving large datasets with string keys.

Trie

A Trie is a tree-like data structure where each node represents a character of a string, and each path from the root to a leaf node represents a string. It is primarily used for efficient retrieval of strings and prefix-based searches in applications like autocomplete, dictionary lookups, and indexing in databases.

Time and Space Complexity

• Search: O(m), where m is the length of the string.
• Insertion: O(m), where m is the length of the string.
• Deletion: O(m), where m is the length of the string.
• Space Complexity: O(N * m), where N is the number of strings and m is the average length of the strings. A Trie can be space-inefficient due to storing each character in a node.

Insertion Process in Trie (Example)

Let's insert the strings "cat", "car", and "dog" into the Trie.

1. Insert "cat":

   • Starting from the root, we insert the characters 'c', 'a', and 't'.
   • The node for 't' is marked as the end of the word.

                       Root
                       /
                      c
                     /
                    a
                   /
                  t [End]

2. Insert "car":

   • Starting from the root, 'c' and 'a' already exist.
   • We insert 'r' and mark it as the end of the word.

                       Root
                       /
                      c
                     /
                    a
                   / \
                  t   r [End]

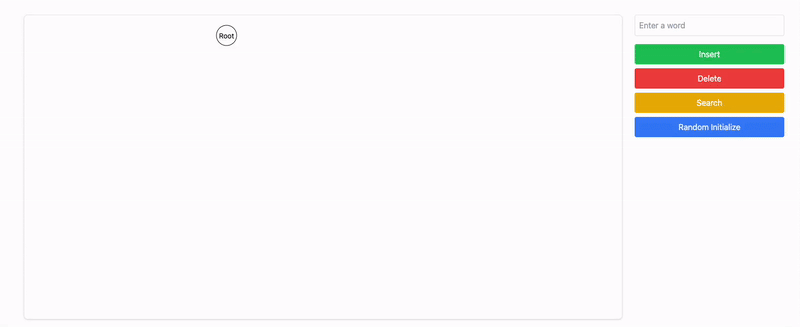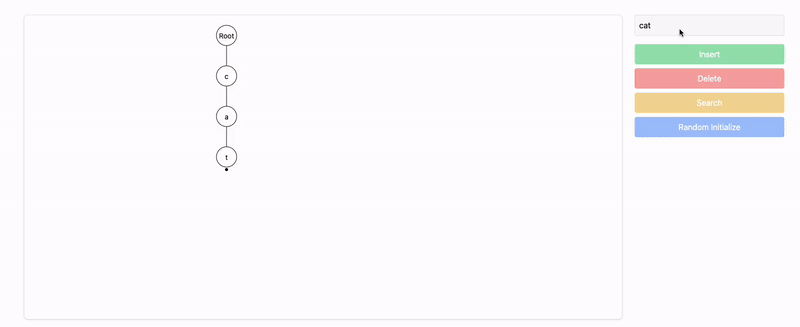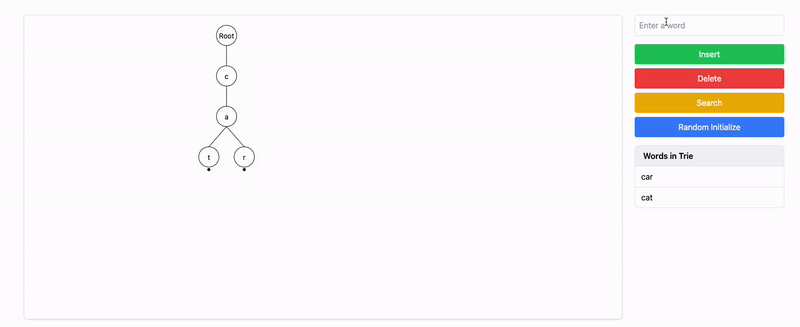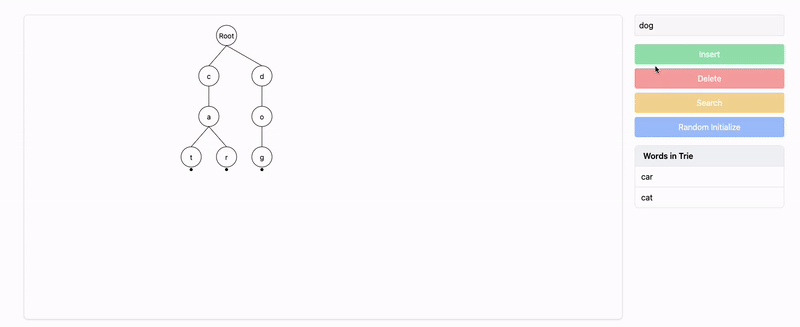
3. Insert "dog":

   • The path for "dog" does not exist, so we insert 'd', 'o', and 'g'.

                          Root
                      /          \
                     c            d
                    /            /
                   a            o
                  / \          /
           [End] t   r [End]  g [End]

Deletion Process in Trie

To delete a string, we follow the path of characters and remove nodes when no other string shares that path.

1. Delete "car":
   • Start at the root and follow the path 'c' -> 'a' -> 'r'.
   • Remove the node for 'r' since it is no longer needed.

                       Root
                       /
                      c
                     /
                    a
                   /
                  t [End]

Search Process in Trie

To search for a string, we traverse the Trie following the characters of the string.

1. Search for "cat":
   • Start at the root and follow the path 'c' -> 'a' -> 't'.
   • Since 't' is marked as the end of the word, the string is found.

Radix Tree (Compressed Trie)

A Radix Tree is a space-optimized version of a Trie. It compresses nodes that have a single child into a single node containing the combined string. This reduces the depth of the tree and the number of nodes, making Radix Trees more space-efficient while maintaining fast lookup times.

Time and Space Complexity

• Search: O(m), where m is the length of the string.
• Insertion: O(m), where m is the length of the string.
• Deletion: O(m), where m is the length of the string.
• Space Complexity: O(N * k), where N is the number of strings and k is the average length of the string segments stored in nodes.

Insertion Process in Radix Tree (Example)

Let's insert the strings "cat", "car", and "dog" into the Radix Tree.

1. Insert "cat":

   • Starting from the root, we insert the string "cat" as a single node.

                       Root
                        |
                       cat [End]

2. Insert "car":

   • "cat" and "car" share the common prefix "ca", so we split the node for "ca" into two branches: one for 't' and one for 'r'.

                       Root
                        |
                       ca
                      /  \
                     t    r [End]

3. Insert "dog":

   • "dog" shares no common prefix with "cat" or "car", so we insert it as a separate node.

                       Root
                        |
                       ca
                      /  \
                     t    r [End]
                          |
                        dog [End]

Deletion Process in Radix Tree

To delete a string in a Radix Tree, we follow the path and remove the node when necessary, merging nodes if they become redundant.

1. Delete "car":
   • Start at the root and follow the path 'ca' -> 'r'.
   • Since 'r' is no longer needed, we remove it and merge the branches.

                       Root
                        |
                       ca
                        |
                       t [End]

Search Process in Radix Tree

To search for a string, we traverse the Radix Tree following the combined string nodes.

1. Search for "cat":
   • Start at the root and follow the node "cat".
   • Since "cat" is marked as the end of the word, the string is found.

Comparison Between Trie and Radix Tree in Database Context

Feature	Trie	Radix Tree
Compression	No compression; each character in a separate node	Compression of single-child nodes
Time Complexity	O(m) for search, insert, delete (m = length of string)	O(m) for search, insert, delete (m = length of string)
Space Complexity	O(N * m), where N is the number of strings and m is the average string length	O(N * k), where k is the average length of compressed string segments
Search Speed	Fast due to prefix-based structure	Fast due to prefix-based structure and compression
Use Cases	Ideal for autocomplete, dictionary search, indexing	Ideal for large datasets with common prefixes, efficient indexing

Real-World Examples in Databases

Full-Text Search Engines

• Trie: Tries are commonly used in full-text search engines such as Elasticsearch, where they help efficiently store and search text data based on prefixes.
• Radix Tree: Radix Trees are often used in databases for prefix-based indexing, where they help store large amounts of text with common prefixes in a space-efficient manner.

Autocomplete and Spell Checking

• Trie: Applications like Google Search, Wikipedia, or Spell Checkers use Tries for real-time suggestions and fast prefix-based searches.
• Radix Tree: For larger datasets with many common prefixes, Radix Trees are used to reduce space consumption and optimize performance.

IP Routing

• Trie: In IP routing, Tries are used to store routing tables where the longest matching prefix determines the routing path for packets.
• Radix Tree: Radix Trees are commonly used in routers to store IP addresses with common prefixes efficiently, optimizing storage and lookup times.

Database Indexing

• Trie: Tries are used in indexing systems to enable fast lookups of string keys and prefix searches.
• Radix Tree: Radix Trees are often used in databases like LevelDB or Berkeley DB for indexing and optimizing lookup times in situations where strings share prefixes.