B-Trees

B-Trees (Balanced Trees) are self-balancing tree data structures widely used in database systems for indexing and efficient data retrieval. They maintain sorted data and allow searches, sequential access, insertions, and deletions in logarithmic time. The B+ Tree, a variant of the B-Tree, is particularly optimized for disk-oriented DBMSs and is the most commonly used type in modern databases.

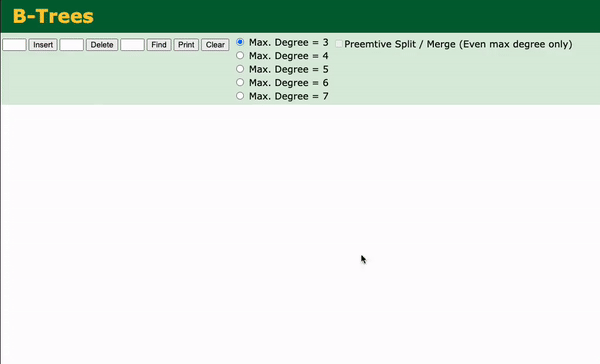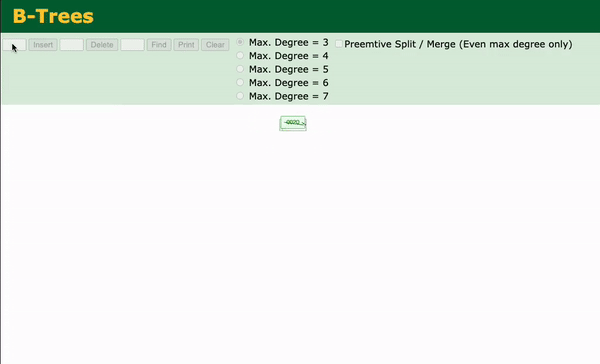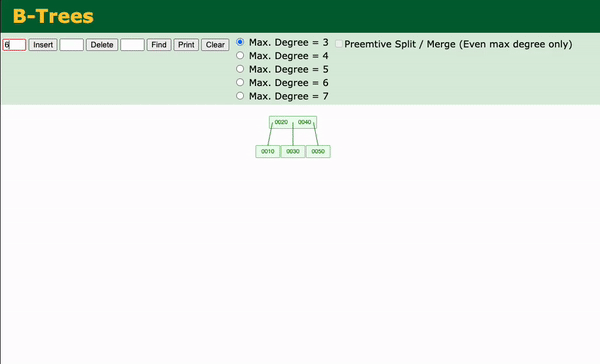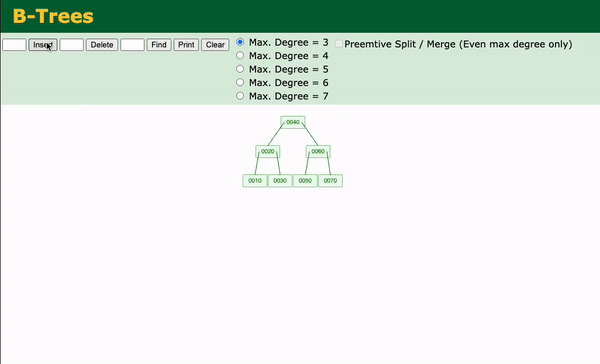
B-Trees: Structure and Operations

A B-Tree of order m (where m is the maximum number of children) has the following properties:

• Each node can contain at most m - 1 keys and m children.
• All leaf nodes are at the same depth, ensuring balance.
• A node with k keys has exactly k + 1 child pointers.
• Keys in each node are sorted.

B+ Trees

The B+ Tree extends the B-Tree with the following modifications:

• Leaf Nodes: All values are stored in the leaf nodes, and internal nodes only store keys for routing.
• Linked Leaves: Leaf nodes are linked sequentially, making range queries more efficient.
• Optimized Disk Access: Larger nodes reduce the number of disk I/O operations.

Feature	B-Tree	B+ Tree
Data Storage	Keys and values in all nodes	Values only in leaf nodes
Range Queries	Less efficient	Highly efficient
Sequential Access	Not supported	Supported via linked leaves

Nodes in B+ Trees

Nodes in a B+ Tree can store data in two primary ways:

1. Storing Record IDs:

   • Keys in the node point to record IDs, which are references to the actual data stored elsewhere (e.g., on disk or in memory).
   • This approach reduces the size of nodes, allowing for more keys to fit in each node, which in turn improves the tree’s depth and efficiency.
   • Suitable for scenarios where fast lookups and space efficiency are priorities.
   • Example Databases: PostgreSQL, MS SQL Server, Oracle DB, IBM DB2

2. Storing Tuple Data:

   • Nodes store the actual data (e.g., entire rows or tuples) alongside keys.
   • This approach simplifies data access since no additional lookups are needed to retrieve data.
   • However, storing tuple data increases the node size, potentially leading to deeper trees and more disk I/O.
   • Example Databases: SQLite, MS SQL Server, MySQL, Oracle DB

B+ Tree Operations

Search in B+ Trees

1. Traverse from Root to Leaf:

   • Start at the root and compare the target key with keys in the current node.
   • Follow the appropriate child pointer based on comparisons until reaching a leaf node.

2. Locate Key in Leaf Node:

   • Search within the leaf node to find the target key. Use binary or linear search depending on the implementation.

Example:

• Target Key: 37
• Tree:
  • Root: [20, 40]
  • Children: [10, 20], [25, 35], [45, 50]
  • Leaf Nodes: [5, 10, 15], [20, 25, 30], [35, 37, 38], [45, 50]
• Process:
  1. Compare 37 with root keys. Follow the child pointer for range 20-40.
  2. Arrive at node [25, 35]. Follow pointer for range 35-40.
  3. Arrive at leaf node [35, 37, 38]. Locate 37.

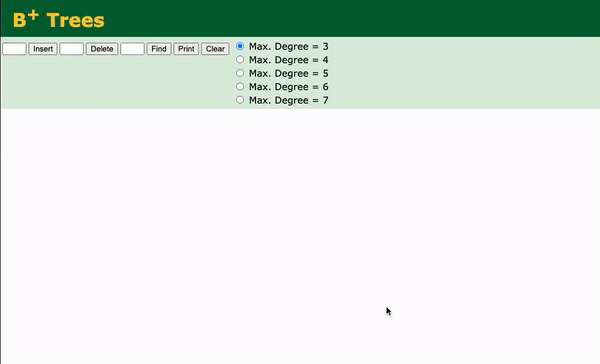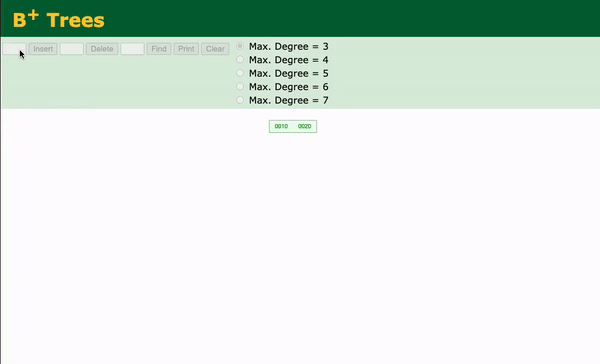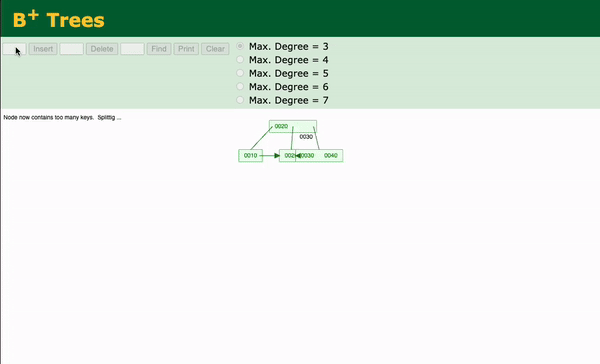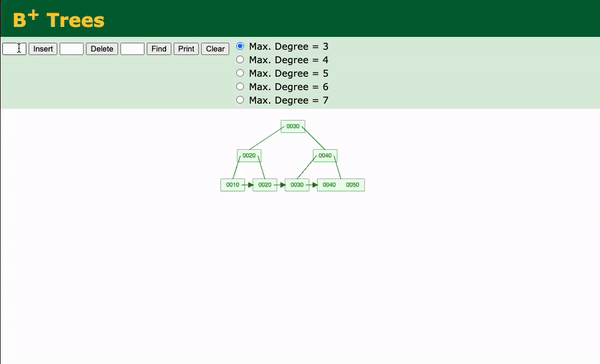
Insertion in B+ Trees

1. Locate the Target Leaf:

   • Traverse the tree from the root to find the appropriate leaf node where the new key should be inserted.

2. Insert the Key:

   • Insert the new key in sorted order within the target leaf node.
   • If the leaf node has enough space, the insertion is complete.

3. Handle Overflow:

   • If the leaf node overflows (i.e., exceeds its maximum capacity), split it into two nodes:
     • Distribute the keys evenly between the two nodes.
     • Promote the middle key to the parent node to act as a separator.
   • If the parent node overflows due to the promoted key, recursively split the parent node and propagate the changes up to the root if necessary.

Example:

• Insert Key: 45
• Initial Tree:
  • Root: [30]
  • Children: [10, 20], [40, 50]
  • Leaf Nodes: [5, 10, 15], [20, 25, 30], [40, 50]
• Process:
  1. Locate leaf node [40, 50].
  2. Insert 45 in sorted order: [40, 45, 50].
  3. Leaf overflows. Split into [40, 45] and [50]. Promote 45 to root.
  4. Updated Tree:
     • Root: [30, 45]
     • Children: [10, 20], [40, 45], [50]

Deletion in B+ Trees

1. Locate the Target Key:

   • Traverse the tree to find the leaf node containing the key to be deleted.

2. Delete the Key:

   • Remove the key from the leaf node.
   • If the leaf node has enough keys to remain valid, the deletion is complete.

3. Handle Underflow:

   • If the leaf node underflows (i.e., contains fewer keys than the minimum required), attempt to rebalance:
     • Redistribute Keys: Borrow keys from a sibling node if it has extra keys.
     • Merge Nodes: If redistribution is not possible, merge the underflowing node with a sibling and remove the separator key in the parent node.
   • If the parent node underflows as a result of the merge, recursively rebalance or merge nodes up to the root if necessary.

Example:

• Delete Key: 25
• Initial Tree:
  • Root: [30]
  • Children: [10, 20], [40, 50]
  • Leaf Nodes: [5, 10, 15], [20, 25, 30], [40, 50]
• Process:
  1. Locate leaf node [20, 25, 30].
  2. Remove 25: [20, 30].
  3. Node remains valid. No further rebalancing needed.
• Final Tree remains unchanged.

Composite Index in B+ Trees

A composite index is a B+ Tree index created on multiple attributes of a table. This allows the database to efficiently handle queries involving combinations of these attributes, offering a balance of performance for both equality and range-based lookups. Composite indexes are particularly useful in scenarios where multi-column filtering is common.

Structure

1. Key Composition:

   • Each composite index key is a concatenation of the indexed attributes in a defined order.
   • For example, a composite index on columns A, B, and C will have keys structured as (A, B, C).

2. Sorting:

   • The keys are stored in a lexicographic order based on the sequence of attributes.
   • This ordering supports efficient prefix-based lookups.

Usage in Queries

• Equality Queries:
  • A query like WHERE A = 1 AND B = 2 directly uses the composite index to locate the matching tuples.
• Range Queries:
  • Queries like WHERE A = 1 AND B BETWEEN 10 AND 20 can leverage the sorted order of the index to quickly retrieve the range.
• Partial Prefix Queries:
  • Queries involving only a subset of the indexed attributes (e.g., WHERE A = 1) can also use the index, but only for attributes up to the prefix.
• Selection Conditions:
  • For queries like WHERE A = 1 AND (B = 2 OR C = 3), composite indexes handle AND conditions efficiently but are limited with OR. Multiple indexes or alternative query optimization techniques might be needed for OR operations.

Benefits

1. Optimized Lookups:

   • Reduces the need for multiple single-column indexes by combining attributes into a single, efficient structure.

2. Faster Range Queries:

   • Allows sequential scans across the leaf nodes, benefiting range-based operations.

3. Reduced Storage Overhead:

   • By consolidating multiple indexes into one, composite indexes save storage space.

Trade-offs

1. Order Matters:

   • The order of attributes in the index affects its usability. An index on (A, B) cannot be used efficiently for queries like WHERE B = 2 alone.

2. Insertion Overhead:

   • Maintaining a composite index during data modifications may slightly increase overhead compared to single-column indexes.

3. Increased Complexity:

   • Requires careful design to ensure that the index order aligns with query patterns.

Duplicate Keys in B+ Trees

Duplicate keys occur when multiple records share the same key value in a B+ Tree index. Managing duplicates efficiently is essential to ensure the index remains compact and performs optimally.

Handling Duplicate Keys

1. Appending Record Identifiers:

   • Store a unique identifier (e.g., a record ID or row pointer) along with each key to distinguish duplicates.
   • This ensures every entry in the tree remains unique while maintaining the ability to retrieve duplicates.

2. Overflow Pages:

   • If a single leaf node cannot hold all duplicates, the tree can use overflow pages to store excess duplicates.
   • Overflow pages are linked sequentially, ensuring duplicates are accessible efficiently.

3. Value Lists in Leaf Nodes:

   • Store duplicates as a list or array within the same leaf node entry, reducing space overhead and simplifying traversal.

Examples

• Example 1: Record Identifiers:
  • Keys: [10, 20, 20, 20, 30]
  • Storage: [10, 20 (RID1), 20 (RID2), 20 (RID3), 30]
• Example 2: Overflow Pages:
  • Keys: [10, 20, 30]
  • Leaf Node for 20: [20] -> Overflow Page: [20, 20, 20]
• Example 3: Value Lists:
  • Keys: [10, 20: [RID1, RID2, RID3], 30]

Benefits

1. Compact Storage:
   • Reduces duplication in storage by consolidating entries.
2. Efficient Retrieval:
   • Allows quick traversal to find all duplicates without scanning unnecessary entries.
3. Scalability:
   • Ensures the index structure remains manageable even with large numbers of duplicates.

Trade-offs

1. Complexity:
   • Managing overflow pages or lists adds complexity to insertions and deletions.
2. Performance:
   • Traversing overflow pages or large value lists may increase retrieval time.

Clustered Indexes

A clustered index organizes the data rows in the table according to the order of the index. Unlike non-clustered indexes, where the data and index are separate, clustered indexes store the data directly in the leaf nodes of the B+ Tree. This close alignment between the index and the physical storage of data improves retrieval performance.

1. Structure:

   • The leaf nodes of the B+ Tree contain the actual data rows instead of pointers to the data.
   • Ensures that the rows are physically sorted according to the index keys.

2. Advantages:

   • Improved Query Performance: Queries that require range scans or sequential access benefit from the physical ordering of data.
   • Space Efficiency: Eliminates the need for an additional structure to store the data, as the index and data are integrated.

3. Limitations:

   • Single Clustered Index: A table can have only one clustered index due to the physical ordering constraint.
   • Insertion Overhead: Maintaining the physical order can lead to page splits and additional write operations during inserts.

4. Example Use Case:

   • A clustered index on OrderDate in a sales table improves performance for queries like SELECT * FROM Sales WHERE OrderDate BETWEEN '2023-01-01' AND '2023-12-31'.

Index Scan Page Sorting

When using a non-clustered index, the data rows are stored separately, leading to potential inefficiencies in retrieving data scattered across multiple pages. Index scan page sorting addresses this issue by optimizing the retrieval process.

1. Process:

   • During an index scan, the database retrieves pointers to the data rows that satisfy the query conditions.
   • The pointers are then sorted by their physical page IDs to minimize random I/O operations.
   • The sorted pointers are used to fetch the data, ensuring each page is accessed only once.

2. Benefits:

   • Reduced Disk I/O: Sorting page IDs minimizes the number of times the database needs to access the same page.
   • Faster Query Execution: Sequentially fetching pages improves performance for large result sets.

3. Example Use Case:

   • A query on a non-clustered index like SELECT * FROM Orders WHERE CustomerID = 123 retrieves all matching rows and sorts the pointers to optimize page access.

Types of B Trees

B Trees and their variants are fundamental to many database and file system implementations. Different types of B Trees have been developed to address specific requirements and workloads. Below are some of the common types and their key features:

1. Standard B Trees

• The original B Tree structure designed to maintain balance and ensure logarithmic time complexity for search, insertion, and deletion.
• Keys and data can be stored in both internal and leaf nodes.
• Suitable for general-purpose indexing but less optimized for range queries compared to B+ Trees.

2. B+ Trees

• A variant of B Trees where all data is stored in the leaf nodes, and internal nodes store only keys for routing.
• Leaf nodes are linked, enabling efficient range queries and sequential scans.
• Most widely used in databases and file systems due to its optimized performance for range-based queries.

3. B* Trees

• An extension of B Trees with higher space utilization by redistributing keys between sibling nodes before splitting.
• Reduces the frequency of node splits, which can improve performance for write-heavy workloads.
• Commonly used in scenarios where minimizing space overhead is critical.

4. Bⁿ Trees (Write-Optimized B Trees)

• Designed for write-heavy applications, these trees buffer changes in memory and propagate them lazily to disk.
• Reduces write amplification by batching updates.
• Suitable for systems with frequent inserts, such as log-structured merge (LSM) trees.

5. Blink Trees

• A variation of B+ Trees that introduces sibling pointers at all levels, not just the leaf level.
• Simplifies concurrency control by allowing nodes to be traversed even when splits are in progress.
• Ideal for distributed systems and environments requiring high concurrency.

6. R Trees

• Specialized tree structure used for spatial data indexing.
• Stores multi-dimensional keys and supports operations like range and nearest neighbor queries.
• Used in geographic information systems (GIS) and CAD applications.

7. Fractional Cascading Trees

• Enhances standard B Trees by embedding auxiliary data structures to speed up multi-level queries.
• Improves performance for certain types of hierarchical queries, such as graph traversals.

Each of these variants addresses specific challenges, making them suitable for different use cases, such as handling large datasets, optimizing writes, or supporting multi-dimensional queries.

Design Choices in B+ Trees

1. Node Size:

   • Disk-Oriented Systems: Larger nodes, typically in the order of kilobytes or megabytes, reduce the number of disk seeks by grouping more data into a single read operation.
   • In-Memory Systems: Smaller nodes, such as 512 bytes or less, fit into CPU cache lines to minimize access latency.
   • Workload considerations play a significant role; point queries favor smaller nodes, while sequential scans benefit from larger nodes.

2. Merge Threshold:

   • Eager Merging: Immediately merge nodes when they underflow. This approach ensures a tightly packed tree but can lead to frequent splits and merges under high update workloads.
   • Lazy Merging: Postpone merging operations until a batch of updates is complete, reducing thrashing and improving overall performance.
   • Some systems, like PostgreSQL, temporarily allow unbalanced trees to batch merge operations later.

3. Variable Length Keys:

   • Pointer-Based Storage: Instead of directly storing large keys, pointers to external storage reduce node size but introduce additional lookups.
   • Fixed-Size Padding: Pads smaller keys to match the size of the largest key, simplifying node management at the cost of memory overhead.
   • Key Map/Indirection: A mapping structure stores keys externally while retaining compact indices within nodes, commonly used in systems like PostgreSQL.

4. Intra-Node Search:

   • Linear Search: Simplest approach with O(n) complexity. Beneficial for small nodes or SIMD optimization.
   • Binary Search: Efficient with O(log n) complexity, requiring sorted keys within nodes.
   • Interpolation Search: Uses metadata (e.g., min/max key values) to estimate the target location. Limited to keys with predictable distributions, such as integers.

5. Clustering of Null Keys:

   • Depending on the index specification, null keys can be clustered at the beginning (NULL FIRST) or the end (NULL LAST) of the leaf nodes, optimizing specific query patterns.

Optimizations in B+ Trees

1. Prefix Compression:

   • Removes redundant prefixes in keys within a node to save space.
   • Useful for lexicographically ordered keys where prefixes like "common" in "commonplace" and "commonly" can be stored once.
   • Reduces memory overhead in workloads with highly similar data.

2. Deduplication:

   • Consolidates duplicate keys by storing them once and maintaining associated values as a linked list or a compact structure.
   • Improves space efficiency for indexes with repeated values, such as boolean flags or category IDs.

3. Suffix Truncation:

   • Truncates keys in internal nodes to their minimal distinguishing prefix to save space.
   • Example: Instead of storing "dog", "dogma", "dogwood" in internal nodes, only store "d", "dogm", and "dogw" for routing purposes.

4. Pointer Swizzling:

   • Converts page IDs into direct memory pointers during tree traversal to reduce buffer pool lookups.
   • Improves performance for in-memory operations, particularly in read-heavy workloads.
   • When a page is evicted, swizzled pointers revert back to their original IDs.

5. Bulk Insert:

   • Constructs the B+ Tree bottom-up by sorting the input data first and inserting it directly into leaf nodes.
   • Minimizes the need for splits and rebalancing during the initial creation phase.
   • Suitable for batch-loading operations, such as initializing indexes for new datasets.

6. Write-Optimized B+ Trees:

   • Variants like Bᵊ-Trees use an in-memory log to buffer changes and periodically propagate them to the main tree.
   • Reduces write amplification, making them ideal for workloads with frequent updates and inserts.

7. Sibling Pointers:

   • Leaf nodes maintain pointers to their immediate neighbors, enabling efficient range scans and sequential access.
   • Reduces traversal time for range queries by skipping intermediate nodes.

8. Cache-Aware Optimization:

   • Designs node sizes to align with CPU cache lines or disk block sizes for optimal memory utilization.
   • Ensures that frequently accessed nodes remain resident in the cache to minimize latency.

9. Parallel Traversal:

   • Enables concurrent access to different subtrees by minimizing contention in the root and upper-level nodes.
   • Useful for large-scale systems where multiple queries access the same index simultaneously.

Advantages

1. Efficient Disk Access: Reduces the number of disk reads and writes by grouping data into large nodes.
2. Scalability: Handles large datasets effectively.
3. Consistent Performance: Balanced structure ensures logarithmic time complexity for operations.
4. Range Queries: Linked leaf nodes in B+ Trees support efficient range-based data retrieval.

Applications in Databases

1. Indexing: Used for primary and secondary indexes, enabling efficient point and range queries.
2. Clustered Indexes: Aligns table storage with index order for faster retrieval.
3. Composite Indexes: Supports multi-attribute queries using composite keys.
4. File Systems: Common in file systems like NTFS and ext4 for metadata and directory indexing.
5. Transaction Systems: Efficiently manages transaction logs and metadata in databases.